Notes on Notes

In which I don't know music theory, but gamely press on

    I figure that it's basically impossible to talk Sondheim without trying to get our head around some basic music theory (at least, it's going to be impossible for me to talk through my next set of observations without it), so I figured I'd pause for a second and talk through some of the building blocks of music we're going to be going into in the next bit of our analysis. I'm going to warn you ahead of time, I have a tin ear, so I'm approaching this from a science-and-math first direction which ends up in the same place, but the path there may look different. Let's go! 

    One of the most important things to understanding how music works is first understanding its most atomic unit - the note. A note is a distinct sound that, when paired with other notes patterned in time, build a musical piece. If motifs are the "words" of music, notes are the individual letters (or perhaps, more accurately, the phonemes the letters decode to.)

    Before we get any further, let's talk about how exactly notes are created. Even if you've never played an instrument before, if you've ever "plucked" a string that was kept taut and heard the twang, you've created a note If you zoom in on what's happening with that vibrating string (or rubber band, or guitar string or piano wire or whatever), is that it's actually vibrating back and forth hundreds if not thousands of times a second . This causes the molecules in the air to be disturbed in the same pattern. Think standing in the center of a swimming pool and jumping up and down - the waves emanate from you in alignment with your up-and-down motion.

    When the sound waves hit our ear, they get converted from the "outer" motion of the sound wave to an "inner" motion in the cochlear fluid via the eardrum which in turn gets transmitted to the brain in a series of electrical pulses which we understand as music.

    So how do we get from our musical phonemes to symphonies? Well, that's going to take some more understanding of the math behind our notes. Let's zoom in again.

    

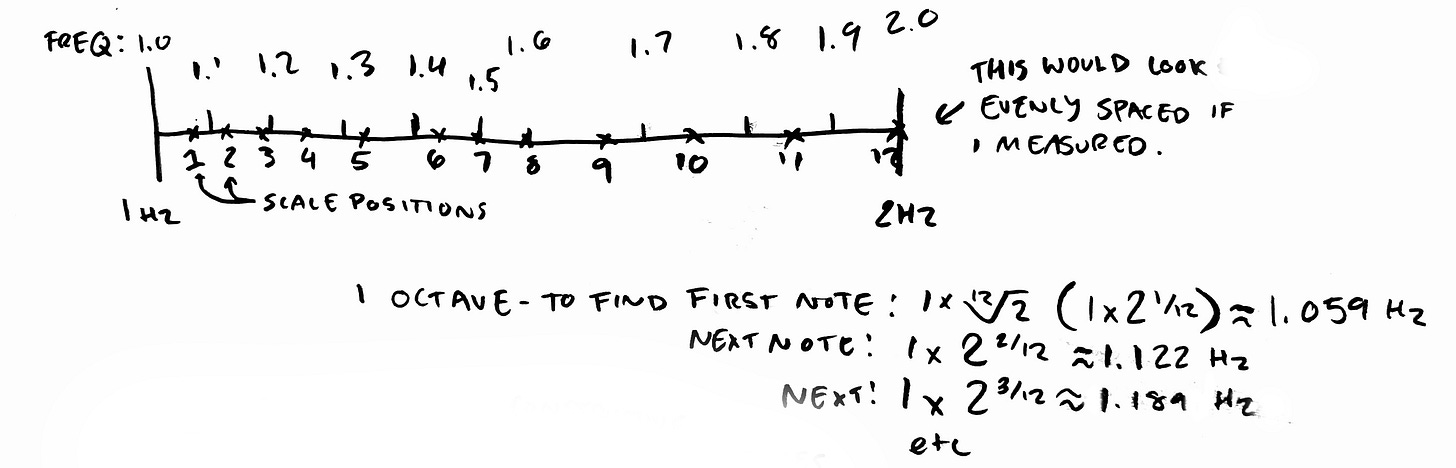
If we were to take a (pure) musical note and plot it along an X/Y axis, with X representing time and Y representing the shifts in air pressure over time, we'd see a sinusoidal wave form appear. If we were to count the number of cycles (complete shifts consisting of a down stroke and an upstroke - basically for every "two halves" of a circle) that occur per second we'd get the frequency of the waveform in hertz. Each musical note sounds distinct because of their frequency. The human ear has a frequency range from about 20 hz to 20,000 hz (20 kHz) and the ability to distinguish between notes at a range of about 1hz. Considering most music is performed somewhere close to the low 1000s/high 100s, that allows for very minute shifts to be registered by the ear.

    Now let's say we have a note with a frequency of 1hz. By itself it doesn't do very much, however, if we were to double the frequency to 2hz we'd notice something peculiar. The new note at 2hz shares some harmonic characteristics of the note at 1hz, just in a higher pitched tone. This brings us to an important notion in music theory - that of octaves. By doubling the frequency of any pitch (or halving it) we arrive at a note that is equivalent to the initial note in harmonic function and musical role. If you're familiar with solfège (or more likely, the Sound of Music), you'd recognize that you start with "Do" (a deer, a female deer) and also end by being "brought back" to "Do". The initial "do" and the final "do" are the same note, an octave apart. It's also worth noting that this principle of doubling frequencies to reach octave equivalence applies to any musical note, not just "Do". Whether it's "Re", "Mi", "Fa", or any other note in the scale, doubling the frequency of these notes will also result in their respective octaves. For example, if a "Mi" is at 300 Hz, doubling it to 600 Hz will produce another "Mi", but one octave higher.

    "What about all the other notes?" I could not possibly hear you ask from the other side of the computer screen. Excellent theoretical question, good theoretical hustle. Before we can answer THAT question though, we first need to ponder one of the mysteries of western music - which is why the octave is split into 12 pieces (which it is) and yet when we discuss a scale (like do-re-mi as above) we're discussing only 7 notes. 7 isn't 12!

    The answer lies in the difference between the chromatic and diatonic scales. The chromatic scale includes all 12 notes within the octave, each separated by a semitone (the smallest interval used in Western music). This scale is what you hear when you play every single key (black and white) in sequence on a piano from one 'Do' to the next.

    On the other hand, the diatonic scale comprises only seven of these twelve notes. These seven notes form the major scale (Do-Re-Mi-Fa-Sol-La-Ti-Do) and are spaced in a specific pattern of whole steps (two semitones) and half steps (one semitone) that creates a pleasing and harmonically functional sequence. The pattern for the major scale is: whole step, whole step, half step, whole step, whole step, whole step, half step. This pattern is what gives the major scale its distinctive sound, and why it feels 'resolved' or 'complete' especially when returning to the octave 'Do.' There are many different interval patterns

    So it all falls back to the semitones. In order to find the semitones that make up an octave you multiply the starting frequency by 2 1⁄12 times to get the next tone up, 2 2⁄12 for the next, all the way up to 2 12⁄12 which of course simplifies to 2, bringing us back to "do". We now have all 12 notes of our octave to do with as we please. Once we have all twelve notes we can pick out the seven frequencies of the diatonic scale by starting from our initial frequency and moving up one semitone for every "half" step, and two semitones for every "whole" step as described above.

    What's interesting here is that this pattern of steps (Whole Whole Half Whole Whole Half Whole) produces harmonically pleasant results regardless of where you start at. If you begin this pattern on any note, you create a major scale in a different key, but with the same pleasing and functional harmonic qualities. This is how the concept of key signatures and transposition works in music, allowing compositions to be adapted into different keys while retaining their harmonic structure.

    You can think of there being infinitely repeating octaves to the "left" and "right" of the octave you're starting in - all of which consist of 12 notes, each of which has infinite "neighbors" of similar harmonic quality in different octaves. "Traversing" these octaves in similarly infinitely repeating patterns are keys (Do Re MI Fa So.../ Whole Whole Half...). This creates in each key a set of "in" tones and "out" tones. The "in tones" work together within a key to produce harmonic (pleasing) results. When writing a piece of music, musicians choose a key so they have a "bank" of notes that they can use to work with. You'll also often see musicians shift keys- re-centering the scale pattern on a new "home note" opening up new harmonic possibilities.

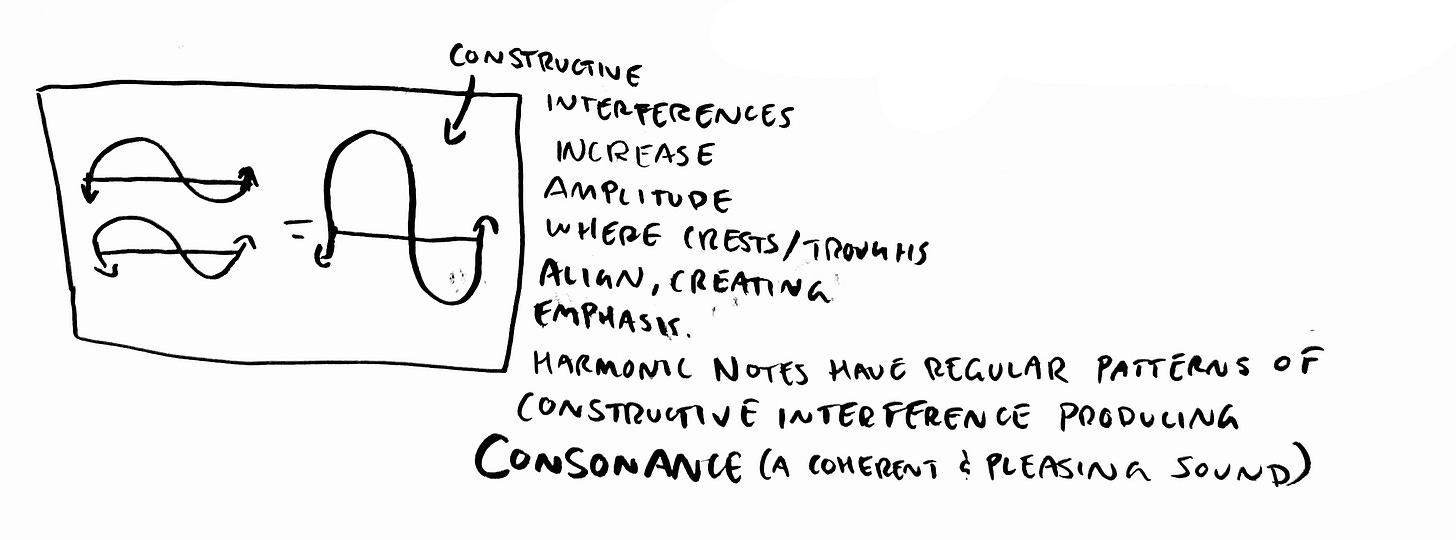
    Playing multiple tones simulatneously produces a chord - although the simplest form of a chord is a dyad (two notes at once), the most common is a triad (three notes at once). Regardless of the number of notes played, what's happening on a waveform level is the same. When notes are played together harmonically, their waveforms align periodically, resulting in a waveform that exhibits regular patterns of constructive interference.

    Constructive interference occurs when two or more waveforms align in phase, meaning their peaks and troughs coincide. When the root, third, and fifth of a chord are played together harmonically, their waveforms align periodically because they are related by simple integer ratios.

    For example, in a major chord, the frequencies of the root, third, and fifth are related by the ratios 4 : 5 : 6 (approximating the perfect fourth, perfect fifth, and major sixth intervals respectively). This means that the waveforms of these notes repeat and align periodically, creating a waveform with regular patterns of constructive interference.

    Visually, when the waveforms align periodically, you would observe distinct peaks and troughs in the combined waveform, corresponding to the aligned peaks and troughs of the individual waveforms. This alignment results in a waveform that exhibits clear periodicity and regularity, indicating harmonic coherence and consonance.

    In contrast, when the waveforms do not align periodically, such as in dissonant intervals or chords, the resulting waveform may appear irregular and chaotic, with less defined patterns of constructive interference. This irregularity reflects the lack of harmonic alignment between the individual waveforms, contributing to the perception of dissonance or tension in the chord. Throughout the course of western music we've identified a number of intervals - patterns of notes within a scale (so a pattern within a pattern within an octave wrapped in an enigma enrobed in dark chocolate) that evoke certain moods. By building a chord out of these intervallic sequences composers can "dial in" sonic mood.

  So let's say you have two notes in your key you're looking to build a chord out of but don't have the third note in your "bank" that would cause it to resolve. A composer can either choose to change keys entirely - re-centering the "home base" of the piece of music to a key that contains the tones necessary OR they can choose to "borrow" the note temporarily. This can either be an "in" tone from a neighboring key or an "out" tone from any key. This process is called tonicization and is often used to create surprise in a piece of music. A composer has to be careful to not overindulge in the process of tonicization lest the music lose its central integrity and fall to discord entirely.